2022-11-16

算法

大O表示法

算法分析的目标是找出问题规模会怎么影响一个算法的执行时间

问题规模是

在前n个整数累计求和中，需要累计的整数个数就是度量问题规模的指标

时间复杂度

眨一下眼	一瞬间
口算29+55	几秒
烧一壶水	几分钟
睡一觉	几小时
完成一个项目	几天/几星期
地球到火星	几年

数量级函数

O(f(n))，其中f(n)表示T(n)中的主导部分

就是说随着T(n)的数量多起来的时候，数据量是影响整个算法完成的主导因素

而不是其他的常数，例如T(n)=n+1中的+1对于计算速度影响微不足道，n的数量才是

python
T(n)=n+1
#当n增大时，常数1在最终结果中显得越来越微不足道，所以可以去掉1，保留n作为主要部分，运行时间的数量级就是O(n)

当n很小时，常数1005起到主导作用影响计算时间

当n越来越大时n²越来越重要，其系数5也不重要了

所以可以去掉27n+1005和系数5，最终时间复杂度O(n²)

这里可以看到时间复杂度的概念是取算法的最差最久的情况中最小的上限所需时间

LIST基本操作的大O数量级

index()	O(1)
index assignment()	O(1)
append()	O(1)
pop()	O(1)
pop(i)	O(n)
insert(i,item)	O(n)
del	O(n)
iteration	O(n)
contains(in)	O(n)
reverse	O(n)
+	O(k)
sort()	O(n log n)

pop() 删除列表最后一项

pop(i)删除列表中间一项

时间复杂度不一致为什么?

删除最后一项无需重新排列列表索引

删除中间一项需要重新将后面的成员索引往前挪一位，时间复杂度n/2去掉系数1/2就是O(n)

字典的大O数量级

copy	O(n)
get item	O(1)
set item	O(1)
delete item	O(1)
contains(in)	O(1)
iteration	O(n)

O(1)<O(logn)<O(n)<O(nlogn)<O(n²)<O(n²logn)<O(n³)

快速判断时间复杂度

确定问题规模n，

循环减半过程logn

k层关于n的循环n^K，两层n的循环就是n²

空间复杂度

空间复杂度用来评估算法内存占用大小的式子

算法使用了几个变量：O(1)

算法使用了长度为n的一维列表：O(n)

算法使用了m行n列的二位列表：O(mn)

线性查找

二分查找

python
import time
'''
线性查找
'''
def get_time(f):

    def inner(*arg,**kwarg):
        s_time = time.time()
        res = f(*arg,**kwarg)
        e_time = time.time()
        print('耗时：{}秒'.format(e_time - s_time))
        return res
    return inner

@get_time
def linear_search(list, value):
    for index, values in enumerate(list):
        if value == values:
            print(value)
            return value
    else:
        return None
linear_search(list(range(10000000)), 64655)


'''
二分查找：
0确定候选区有值
1确定最左端
2确定最右端
3确定中间
4中间值与目标值比较
5若大于目标值，最右端=中间值-1
6若小于目标值，最左端=中间值+1
7若等于返回中间值
7都不满足返回None
'''
@get_time
def binary_search(list, value):
    left = 0
    right = len(list) - 1
    while left <= right:
        mid = (left + right) // 2
        if list[mid] == value:
            return mid
        elif list[mid] > value:
            right = mid -1
        else:
            left = mid +1
    else:
        return None
print(binary_search(range(99999999999), 43955479))

2022-11-17

列表排序

使用内置函数sort()

常见排序算法

冒泡排序	快速排序	希尔排序
选择排序	堆排序	计数排序
插入排序	归并排序	基数排序

冒泡排序(bubble sort)

列表中相邻两个数，如果前面的比后面大，则交换这两个数

一趟下来，无序区减少一个数，有序区增加一个数

第一趟有序区是最后一个数索引为n，无序区是索引0~(n-1)

第二趟有序区是n-1n, 无序区是0(n-2)

总共需要n-1趟，代码关键点：第i趟，箭头在n-i-1， 无序区范围, 第i趟无序区范围是0~(n-i), 有序区范围是n~(n-(i+1))，

python
'''
冒泡排序：传入一个无序列表，循环一个趟数，
如果第i趟列表已经是有序的，无需再循环
循环一个动态指针，比较指针指向的数是否大于后面一个数
如果成立交换彼此的位置
时间复杂度O(n²)，两层关于n的循环
'''
import random

@get_time
def bubble_sort(arr):
    for i in range(len(arr)-1):#第i趟
        isexchange = False#默认列表无序
        for j in range(len(arr)-i-1):#箭头
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
                isexchange = True#找到相邻的数并升好序
        print("第" + str(i) + "趟" +str(arr))
        if not isexchange:#如果一趟下来没找到
            return
arr = [random.randint(0, 10000) for i in range(1000)]
# print(arr)
bubble_sort(arr)
print(arr)

选择排序(select sort)

• 第一趟排序记录最小的数，放到第一个位置
• 第二趟排序记录无序区最小的数，放到第二个位置
• ......
• 第N趟排序记录无序区最小的数，放到第N个位置
• 算法关键点：有序区和无序区，无序区最小值的位置

python
'''
选择排序：参入一个无序列表，循环n-1次
最小值为索引i的值
循环无序区为i+1~列表长度
如果无序区中的数j比最小值小
则j是新的最小值
第i次的数比i+1的数大，交换彼此位置
时间复杂度O(n²)
'''
import random


def select_sort(list):
    for i in range(len(list)-1):
        minValue = i
        for j in range(i+1, len(list)):
            if list[j] < list[minValue]:
                minValue = j
        if minValue != i:
            list[i], list[minValue] = list[minValue], list[i]
list = [random.randint(0, 10000) for i in range(1000)]
select_sort(list)
print(list)

插入排序（insert sort）

• 初始手里只有一张牌（）有序区

• 每次摸一张牌（从无序区），插入到手里的正确位置

  python
  import random
  def insert_sort(list):
      for i in range(1, len(list)):
          catched = list[i]
          onhand = i - 1
          while onhand >= 0 and list[onhand] > catched:
              list[onhand+1] = list[onhand]
              onhand -= 1
          list[onhand+1] = catched
          print(list)
  
  
  list = [random.randint(0,999) for i in range(50)]
  insert_sort(list)
  

快速排序quick sort

快速排序思路：

• 取一个元素p（列表中第一个元素），使元素p归位
• 列表被p分成两部分，左边都比p小，右边都比p大
• 递归完成排序

1. 选定中心轴，通常列表的第一个元素
2. 将大于中心轴的数字放在中心轴右边
3. 将小于中心轴的数字放在中心轴的左边
4. 分别对左右子序列重复上述三个步骤

快排框架

python
def quick_sort(list, left, right):
	if left ＜ right:
		mid = partition(list, left, right)
		quick_sort(list, left, mid-1)
		quick_sort(list, mid+1, right)

修改递归深度：

python
import sys
sys.setrecursionlimit(100000)#修改递归最大深度100000

python
# -*- coding: utf-8 -*-
# @Time : 2022/11/17 17:42
# @Author : ciskp
# @Email : noEmail@qq.com
# @Describe :
def quick_sort(list, left, right):
    mid = list[left]
    while left < right:
        #初次切确定被切列表大于等于两个成员
        while left < right and list[right] >= mid:
        # 右半边的子列表确定大于等于两个成员且最右边的值大于等于mid被比较值
            right -= 1
            #上面的条件满足说明没找到比mid小的值，下标往左移动1位
        list[left] = list[right]
        #上面的while条件不满足说明left和right重合或者找到比mid小的值，故赋值给left的空位
        while left < right and list[left] <= mid:
        # 坐半边的子列表确定大于等于两个成员且最左边的值小于等于mid被比较值
            left += 1
            #上面的条件满足说明没找到比mid大的值，下标往右移动1位
        list[right] = list[left]
    list[left] = mid
    return left

import random
def quick_sort_recursion(list, left, right):
    if left < right:
        mid = quick_sort(list, left, right)
        quick_sort_recursion(list, left, mid-1)
        quick_sort_recursion(list, mid+1, right)
list = [random.randint(0, 99) for i in range(99)]
quick_sort_recursion(list, 0, len(list)-1)
print(list)

**快排效率：**平均时间复杂度O(nlogn)，最坏时间复杂度O(n²)

2022-11-18

归并排序

python
def merge_sort(list, low ,mid, high):
    i = low
    j = mid + 1
    temp = []
    while i <= mid and j <=high:
        if list[i] < list[j]:
            temp.append(list[i])
            i += 1
        else:
            temp.append(list[j])
            j += 1
    while i <= mid:
        temp.append(list[i])
        i += 1
    while j <= mid:
        temp.append(list[j])
        j += 1
    list[low:high+1] = temp

list = [2,4,5,7,1,3,6,8]
merge_sort(list, 0, 3, 7)
print(list)

时间复杂度：O(nlogn)

练习

python
def anagram(s, t):
    ss = list(s)
    tt = list(t)
    ss.sort()
    tt.sort()
    print(ss==tt)
    return ss == tt

s='anagram'
t='nagaram'
anagram(s,t)

2022-11-22

链表linked list

链表是由一系列节点组成的元素集合，每个节点包含两部分，

数据域和指向下一个节点指针next， 通过节点之间的互相连接

最终串联成一个链表

链表的入口节点称为链表的头结点也就是head

最后一个节点的指针域指向null（空指针的意思）

链表有三个属性：当前节点cur，当前节点值cur.data，当前节点指针cur.next

python
'''
206. Reverse Linked List
Input: head = [1,2,3,4,5]
Output: [5,4,3,2,1]
Input: head = [1,2]
Output: [2,1]
Input: head = []
Output: []
双指针
先定义一个空节点，为了反转后最后一个节点指向空
定义当前节点pre
循环当前节点cur不为空，为空代表遍历到链表末尾结束
用一个临时节点temp记录即将被断开的链表从当前节点的指针开始
反转当前节点的指针指向上一个空节点pre
将循环的pre节点往前一位等于cur
将cur往前移动一位等于temp
最后cur为空代表已经遍历完，最后一个元素指针指向空
返回pre为新链表的头部
'''
def reverseLinkedlist(head):
    pre = None
    cur = head
    while cur!=None:
        temp = cur.next
        cur.next = pre
        pre = cur
        cur = temp
    return pre

单链表 双链表

循环链表

遍历查询

python
class Node():#链表定义
    def __init__(self, item):
        self.item = item
        self.next = None#指向下一个成员的指针

a = Node(1)
b = Node(2)
c = Node(3)
a.next = b#链表的查询
b.next = c
print(a.next.item)

创建链表

python
class Node():
    def __init__(self, item):
        self.item = item
        self.next = None  
        # 指向下一个成员的指针

#头插法
def linked_list_head(list):
    head = Node(list[0])
    for element in list[1:]:
        node = Node(element)  
        # 使用Node()创建(初始化)一个新的节点
        node.next = head  # 定义指针
        head = node  # 定义头部
    return head  # 返回新的头部

#尾插法
def linked_list_tail(list):
    head = Node(list[0])
    tail = head
    for element in list[1:]:
        node = Node(element)  
        # 使用Node()创建(初始化)一个新的节点
        tail.next = node  # 定义指针
        tail = node  # 定义头部
    return head  # 返回新的头部


def print_linkedlist(lk):
    while lk:
        print(lk.item, end=',')
        lk = lk.next

lk = linked_list_head([1, 2, 3])
print_linkedlist(lk)

插入

python
p.next = curNode.next#curnode的下一个节点赋值给p
curNode.next = p#将p赋值给curnode，就将新节点p加入到列表中

删除

python
curNode.next = curNode.next.next
#将原来curNode的下两个节点赋值给curnode，等价于删除了原来中间的节点
del p
#可不加这句

# Definition for singly-linked list.
class ListNode:
     def __init__(self, val=0, next=None):
         self.val = val#当前节点值
         self.next = next#当前节点指针
def removeElement(list, val):
	cur = dummy_head = ListNode(next=head)
    #定义一个虚拟节点,将指针指向原来的头部值
    #定义当前节点，不影响原来的链表
    while cur.next != None:
    #当前的下一个节点不指向None时候执行
        if cur.next.val == val:
        #如果当前的下一个节点
        #(从原来的链表第一个开始)的值等于目标值
			cur.next = cur.next.next
            #当前节点的指针指向下下一个节点
        else:
            cur = cur.next
            #如果不等于目标值，当前节点移动到下一个节点
    return dummyNode.next
    #一波循环完毕返回虚拟节点的指针，即新的链表入口
'''
虚拟节点法删除总结：
定义一个虚拟节点，将指针指向原来的头部值
定义一个当前节点为虚拟节点
判断当前节点的指针不指向空开启循环
如果当前节点的指针指向的值等于目标值(要删除的值)
	成立：将当前节点的指针指向当前节点的下两个值
	不成立：将当前节点移向下一个节点指针
最后当前指针指向空一趟循环完毕，返回虚拟节点的指针，就是新链表入口，被删除的元素没有指针指向会被python内存回收机制定时清理
'''

合并两个有序链表

python
'''
21. Merge Two Sorted Lists
Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]

Example 2:

Input: list1 = [], list2 = []
Output: []

Example 3:

Input: list1 = [], list2 = [0]
Output: [0]

创建一个新链表和虚拟节点并初始化链表属性
循环当两列表同时不为空时
如果链表1的值小于链表2的值
      将虚拟节点的指针指向链表1
      链表1向后移动一位以达到遍历效果
上述条件不满足
      虚拟节点的指针指向链表2
      链表2向后移动一位以达到遍历效果
虚拟节点向后移动一位以达到串联新链表效果
如果链表1不为空，则链表2先被遍历完，虚拟节点指针指向链表1的最后一个值
如果链表2不为空，则链表1先被遍历完，虚拟节点指针指向链表2的最后一个值
最后由于虚拟节点指针指向最后一个元素不能代表新链表的入口，所以返回新节点的指针
'''
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next
class Solution:
    def mergeTwoLists(self, list1, list2):
        newhead = dummyhead = ListNode()
        while list1 and list2:
            if list1.val < list2.val:
                dummyhead.next = list1
                list1 = list1.next
            else:
                dummyhead.next = list2
                list2 = list2.next
            dummyhead = dummyhead.next

        if list1:
            dummyhead.next = list1
        elif list2:
            dummyhead.next = list2
        return newhead.next

移除链表重复元素

python
'''
83. Remove Duplicates from Sorted List

'''
# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:
        '''
        初始化当前节点为头结点
        循环当前节点不为空和当前节点的指针不指向空，
        如果当前节点的值等于下一个节点值，将当前节点的指针指向下下个节点
        如果不成立当前节点往前移动一位
        返回去重后的头结点
        '''
        curr=head
        while curr and curr.next:
            if curr.val == curr.next.val:
                curr.next = curr.next.next
            else:
                curr = curr.next
        return head

双链表的插入

python
class Node():
    def __init__(self, item):
        self.item = item
        self.next = None
		self.prev = None#双链表，指向上一个成员的指针
a = Node(1)
b = Node(2)
c = Node(3)
a.next = b
b.next = c
print(a.next.item)

p.next = curNode.next#1
curNode.next.prev = p#2
p.prev = curNode#3
curNode.next = p#4

双链表的删除

python
p = curNode.next
curNode.next = p.next
p.next.prev = curNode
del p

链表和列表的区别

链表插入和删除快于列表，链表内存可以更灵活分配

哈希表hash

Hash Table，称为散列表，是一种线性表的存储结构，

哈希表由一个直接寻址表和一个哈希函数组成，

哈希函数h(k)将元素关键字k作为自变量，返回元素的存储下标

判断一个元素是否出现过的场景应该想到哈希法

什么时候用hash table
列表	数据量小，且值连续
集合	数据量大，值是跳跃的
字典

列表作为哈希表

python
'''
给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

示例 1: 输入: s = "anagram", t = "nagaram" 输出: true

示例 2: 输入: s = "rat", t = "car" 输出: false

说明: 你可以假设字符串只包含小写字母。
'''
def isAnagram(s, t):
    record = []
    for i in range(len(s)):
       	record[ord(s[i])-ord("a")] += 1
	for j in range(len(t)):
		record[ord(j[j])-ord("a")] -= 1
    for k in record:
        if k != 0:
            return True
    return False
'''
定义一个26长度全0的列表一一对应任意小写字母，
循环第一个字符串的长度次，第一个子字符串的acsii码-字符串a的acsii码再加1，即当前子字符串出现次数+1
循环第二个字符串的长度次，第一个子字符串的acsii码-字符串a的acsii码再减1，即当前子字符串出现次数+(-1)
循环最初定义的列表，如果有一个元素不等于0，返回false，否则返回true
'''

python
'''
两数之和
1. Two Sum
Example 1:
Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Example 2:
Input: nums = [3,2,4], target = 6
Output: [1,2]

Example 3:
Input: nums = [3,3], target = 6
Output: [0,1]
由于需要记录遍历过的列表值和出现的次数，故使用字典记录
循环枚举列表的key和value
如果目标值减去当前枚举的值在字典中出现过
返回列表目标值减去当前循环的值
上述条件不存在则添加一个下标为v的k值
如果训话完毕没找到返回空列表[]
'''


def twoSum(nums, target):
    record = {}
    for k, v in enumerate(nums):
        if target - v in record:
            return [record[target- v], k]
        record[v] = k
    return []

哈希冲突

由于哈希表的大小是有限的，但是存储的值是无限的，

因此对于任何函数，都会出现两个不同元素映射到同一个位置上的情况，这就叫做哈希冲突

解决：开放寻址法

如果哈希函数返回的位置已经有值了，则可以向后探查新的位置来存储这个值

1. 线性探查，如果位置i被占用，则探查i+1, i+2......
2. 二次探查，如果位置i被占用，则探查i+1², i-1², i+2², i-2²......
3. 二次哈希，有n个哈希函数，当使用第一个哈希函数h1冲突时，则尝试使用h2，h3

拉链法

哈希表每个位置都连接一个链表，当冲突发生时，冲突的元素将被加到该位置链表的最后

栈stack

栈stack是一个数据集合，可以理解为只能在一端进行插入或删除的列表，栈可以形象理解为堆，书堆，土堆

• 后进先出LIFO(last in , first out )
• 栈顶，栈底
• 栈的基本操作
  • 进栈（压栈）：push (list.append)
  • 出栈pop (list.pop)
  • 取栈顶gettop (list[-1])

python
class stack:
	def __init__(self):
		self.stack = []
    def push(self, element):
        self.stack.append(element)
        
    def pop(self):
        return self.stack.pop()
    
    def get_top(self):
		if len(self.stack) > 0:
			return self.stack[-1]
        else:
            return "empty stack found!"

栈与队列区别

使用栈实现队列

python
'''
232. Implement Queue using Stacks
'''
class MyQueue:

    def __init__(self):
        '''
        用两个栈来表示队列的方法
        '''
        self.stackIn, self.stackOut = [], []
    
    def push(self, x: int) -> None:
        '''
        根据队列先进先出的原理，在入栈列表追加元素
        '''
        self.stackIn.append(x)

    def pop(self) -> int:
        self.peek()
        return self.stackOut.pop()

    def peek(self) -> int:
        '''
        先确定出栈为列表，
        再循环入栈不为空列表，
        出栈列表追加入栈的最后一个元素，并删除它
        返回出栈的最后一个元素
        根据栈的原理后进先出，含1，2，3的栈，出栈后是3，2，1，即1是我们要取的对象
        '''
        if self.stackOut == []:
            while self.stackIn != []:
                self.stackOut.append(self.stackIn.pop())
        return self.stackOut[-1]
    
    def empty(self) -> bool:
        '''
        两个列表都为空则为True，都不为空为False，其中之一不为空为True
        '''
        return not (self.stackIn or  self.stackOut)

最小栈

python
'''
155. Min Stack
'''
class MinStack:
    '''
    使用元组(x,y)这个整体作为列表的元素，x是输入元素，y是最小元素
    '''
    def __init__(self):
        self.stack = []
        
	# 追加最小元素，如果此次元素比栈中最小元素还小，直接插入该元素
    def push(self, val: int) -> None:
        if self.stack:
            self.stack.append((val, min(val, self.getMin())))
        else:
            self.stack.append((val,val))

    def pop(self) -> None:
        if self.stack:
            self.stack.pop()
	# 获取栈顶的元素
    def top(self) -> int:
        if self.stack != []:
            top = self.stack[-1][0]
            return top
        else:
            return
	# 获取最小元素，即列表最后一个元组中第2个元素
    def getMin(self) -> int:
        if self.stack != []:
            getMin = self.stack[-1][1]
            return getMin
        else:
            return
        


# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(val)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()

堆heapq

自带排序功能的数据结构——堆。

python
heapify(list)# 将列表转换为堆
heappush(list,value)# 将value加入到堆的最后面相当于append
heappop(list)# 将堆中最小的一个元素删除

队列queue

Implement Stack using Queues

python
class MyStack:

    def __init__(self):
        self.queueIn = [] 
        self.queueOut = []

    def push(self, x: int) -> None:
        self.queueIn.append(x)

    def pop(self) -> int:
        self.top()
        return self.queueOut.pop(-1)

    def top(self) -> int:
        if self.queueOut == [] or self.queueIn != []:
            while self.queueIn != []:
                self.queueOut.append(self.queueIn.pop(0))
        return  self.queueOut[-1]

    def empty(self) -> bool:
        return not (self.queueIn or self.queueOut)

# Your MyStack object will be instantiated and called as such:
# obj = MyStack()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.top()
# param_4 = obj.empty()

1. 队列Queue是一个数据集合，仅允许在列表一端进行插入，另一端删除
2. 进行插入的一端称为队尾，插入动作叫作进队或入队
3. 进行删除的一端称为对头，删除的动作成为出队
4. 队列性质：先进先出（First in， First out）

属性

• 队首指针前进1：front = （front+1）%MaxSize
• 队尾指针前进1：rear = （rear+1）%MaxSize
• 对空条件：near == front
• 队满条件：（rear+1）%MaxSize == front

二叉树

根节点、叶子节点署到深度（高度）

数的度：2（某个节点拥有最多的子节点数量）

孩子节点/父节点

子树

链式存储，顺序存储

链式用指针，顺序用列表(链式存储就是用指针把分布在散落的地址的子节点串联起来，顺序存储的元素内存是连续分布的)

链式存储如图：

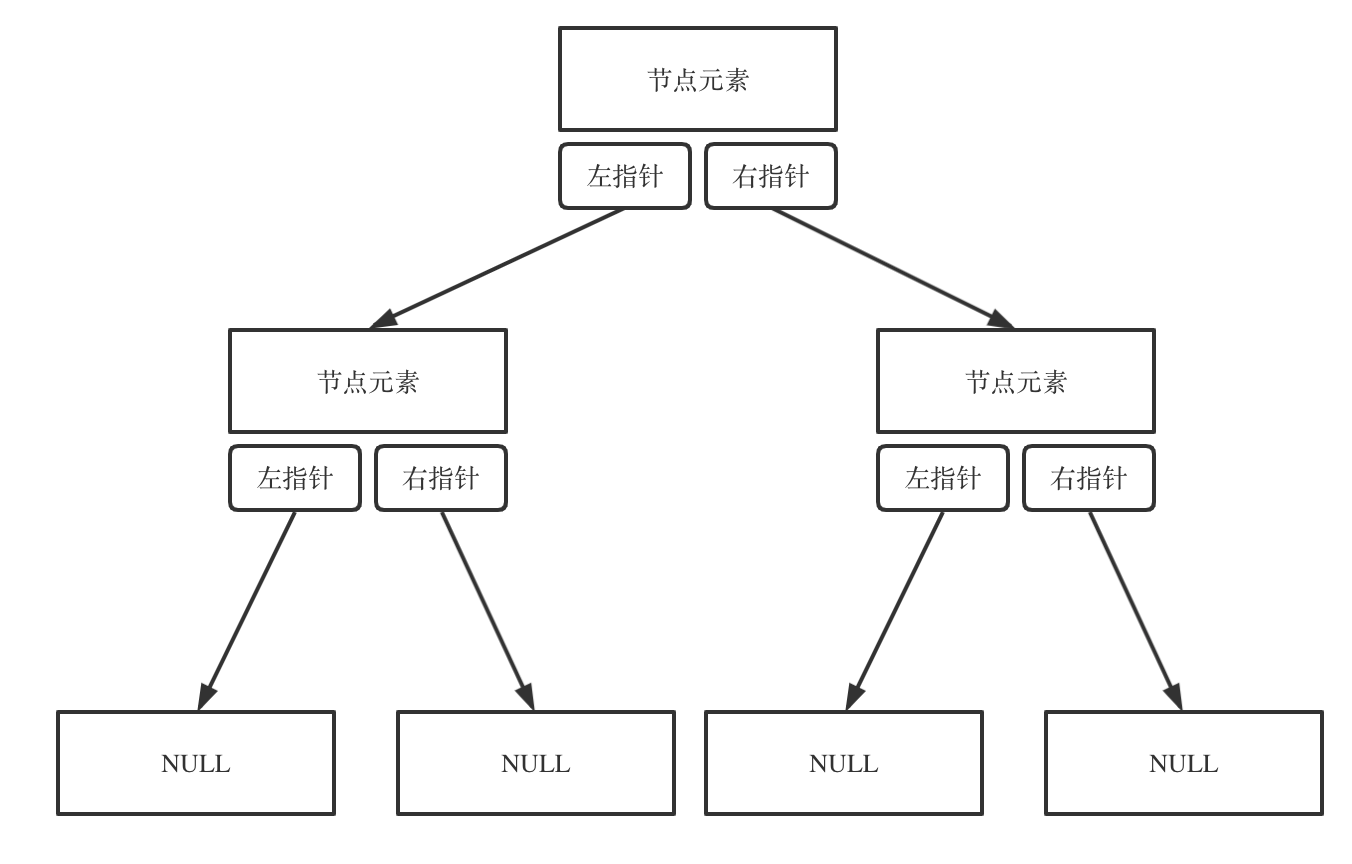
顺序存储的方式如图：

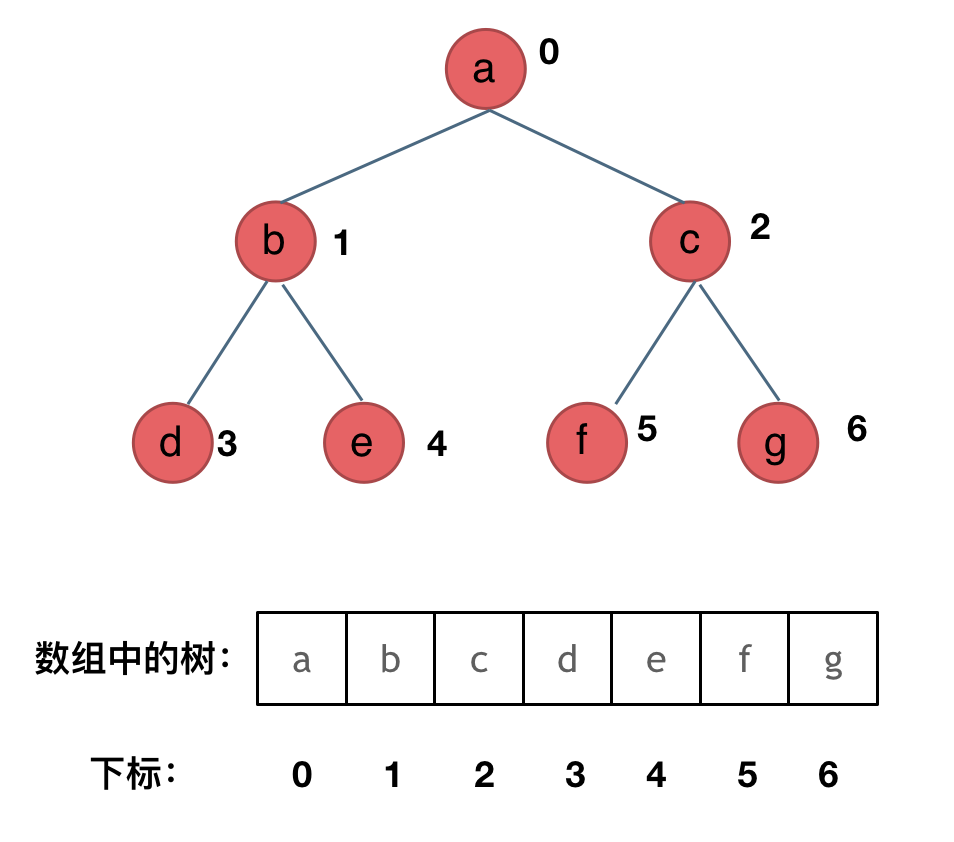
用数组来存储二叉树如何遍历的呢？

如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

满二叉树

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

如图所示：

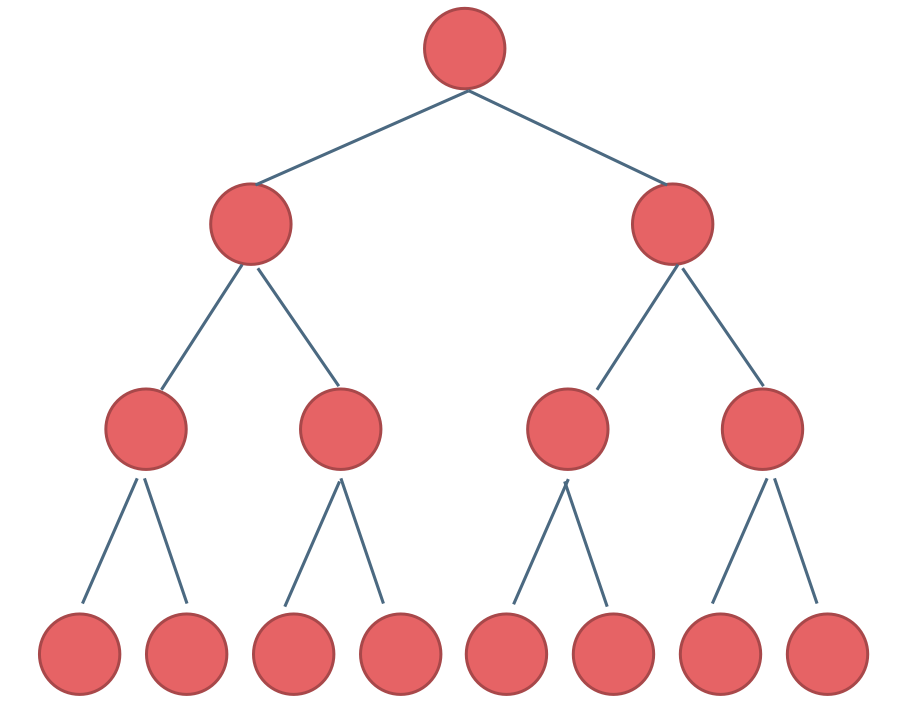
这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。

完全二叉树

什么是完全二叉树？

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，

并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

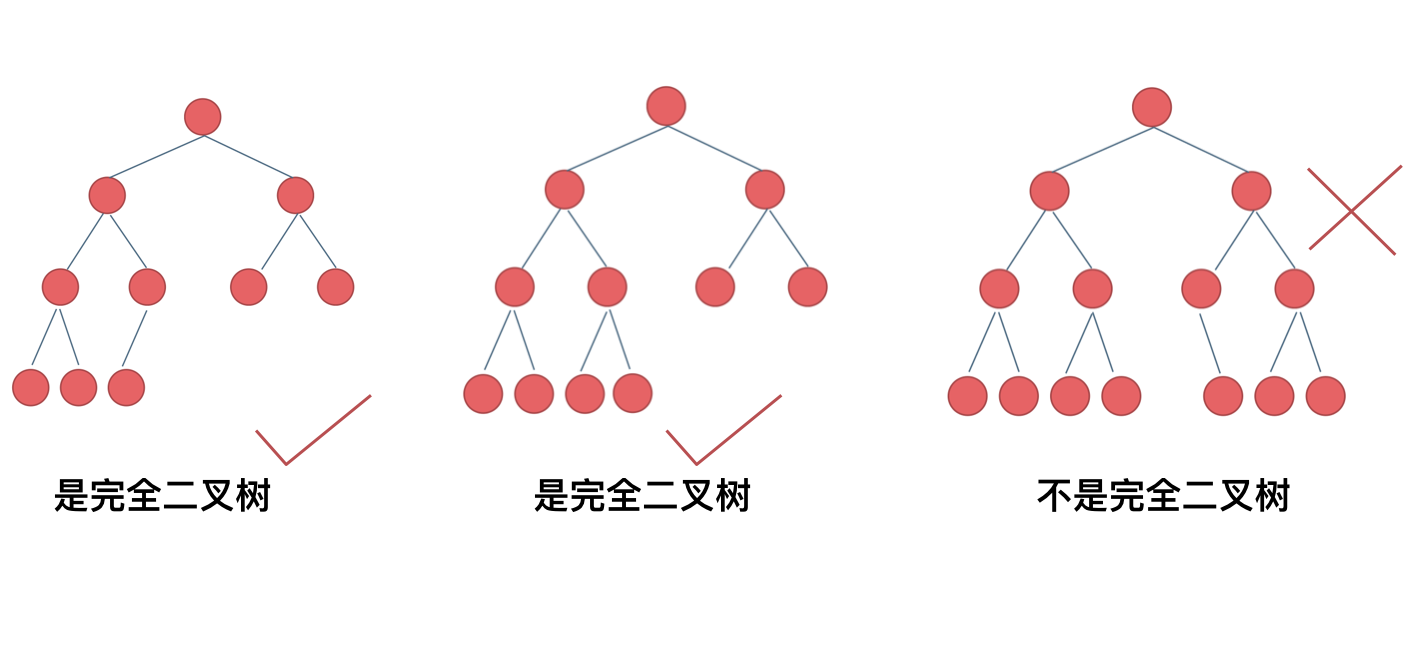
二叉搜索树(左小右大)

前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树

下面这两棵树都是搜索树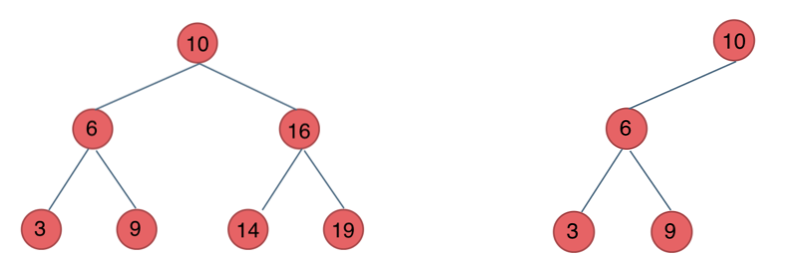

平衡二叉搜索树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：

它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，

并且左右两个子树都是一棵平衡二叉树。

如图：

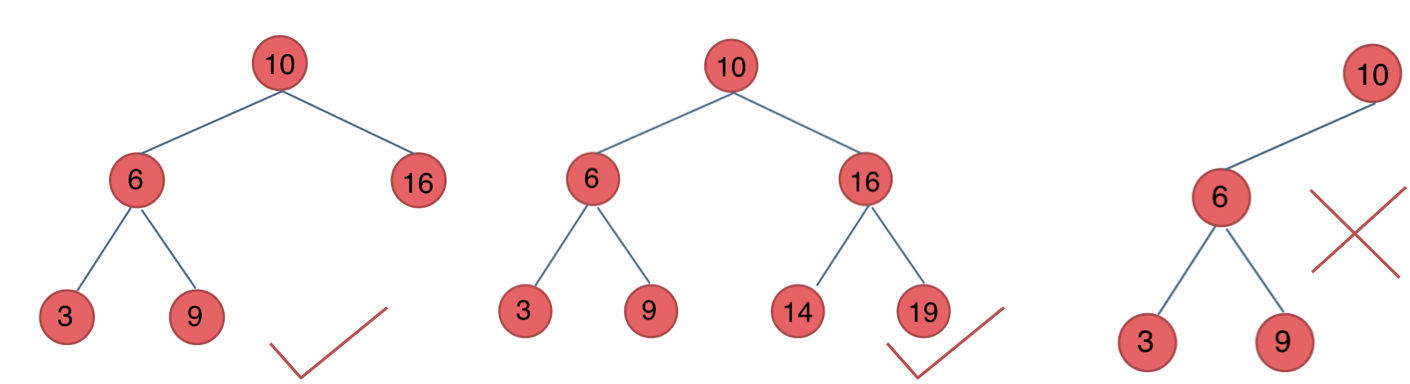
最后一棵 不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。

二叉树两种遍历

1. **深度优先遍历（DFS or Depth-First Search）：先往深走，遇到叶子节点再往回走。
   1. 前序遍历：中左右
   2. 中序遍历：左中右
   3. 后序遍历：左右中
2. 广度优先遍历（BFS or Breadth-First Search）：一层一层的去遍历，而广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。

python
class TreeNode: #二叉树的定义，binary tree definition
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

判断是否平衡二叉树

python

2023-1-12

二叉树的最大深度

使用前序遍历（中左右）求深度，使用后序遍历（左右中）求高度 前深后高

深度优先递归函数定义def dfs(root): depth firsr search

广度优先递归函数定义def bfs(root): breadth first search

• DFS or Depth-First Search
• BFS or Breadth-First Search

2022-11-25

双指针

又称快慢指针法：通过一个快指针和慢指针再一个for循环下完成两个for循环动作

快指针：寻找不含有目标元素的下标

慢指针：不含目标值的新数组的下标

快指针永远负责找即判断目标值，慢指针负责记录，找到一个丢给慢指针覆盖，以此循环

普通双指针从数组或字符串两端同时向中间遍历

python
'''
Input: nums = [3,2,2,3], val = 3
Output: 2, nums = [2,2,_,_]
Input: nums = [0,1,2,2,3,0,4,2], val = 2
Output: 5, nums = [0,1,4,0,3,_,_,_]
上面意思是删除列表中元素3，并返回新列表长度
'''
def removeElement(list, target):
        slowIndex = 0
        #定义慢指针，不含目标值的列表指针
        for fastIndex in range(len(list)):
        #让快指针动起来，像下面图片一样，动的范围从0-原列表长度，左闭右开
            if list[fastIndex] != target:
            #如果快指针指向的值不等于目标值，就是说不含目标值的新数组成员找到一个
                list[slowIndex] = list[fastIndex]
                #将快指针指向的值搬过来赋给慢指针的值，此步骤就是删除目标值
                slowIndex += 1
                #删除完了之后，慢指针往前走一步，循环完了之后，
                #慢指针的值就是新列表的长度，因为它指向最后一个非目标值的索引位
        return slowIndex

python
'''
Input: nums = [1,1,2]
Output: 2, nums = [1,2,_]
Input: nums = [0,0,1,1,1,2,2,3,3,4]
Output: 5, nums = [0,1,2,3,4,_,_,_,_,_]
Given an integer array nums sorted in non-decreasing order,
remove the duplicates in-place such that each unique element appears only once.
The relative order of the elements should be kept the same.
'''

# 双指针法
def removeDuplicates(nums):
    slowIndex = 0
    # 定义慢指针
    for fastIndex in range(1, len(nums)):
        # 定义快指针，从1开始，为了和慢指针比较是否相等
        if nums[slowIndex] != nums[fastIndex]:
            # 如果慢指针的值不于快指针的值，说明慢指针处有需要删除的目标值
            # 不能用等于判断，因为不知道与slowIndex的值相等的最后一个值，
            # 但是知道不等于它的第一个值，此时slow到fast的区间就是需要删除的区域
            # 如果用等于判断，会使相等的值放在连续的位置上
            slowIndex += 1
            # 慢指针往前移动一位为了替换（删除）第二个重复的slowIndex的值
            nums[slowIndex] = nums[fastIndex]
            # 将快指针的值赋给慢指针。完成第二个重复的slowIndex的值的删除
    print(nums)
    return slowIndex + 1
    # 为什么要+1，因为fastIndex循环了n-1次，没有从第0位开始，而列表长度为n，
    # 故+1，加上第一个元素的索引个数


# removeDuplicates([0, 0, 1, 1, 1, 2, 2, 3, 3, 4])


# 暴力破解brute force,空间复杂度不满足O(1)，为O(n)
def bruteForce(nums):
    return list(set(nums))
# bruteForce([0, 0, 1, 1, 1, 2, 2, 3, 3, 4])
# bruteForce([1,1,2])


def hardDelete(nums):
    for i in reversed(range(1, len(nums))):
        if nums[i] == nums[i-1]:
            nums.pop(i)
    print(nums)
    return len(nums)
hardDelete([0, 0, 1, 1, 1, 2, 2, 3, 3, 4])

python
'''
844. Backspace String Compare
Example 1:
Input: s = "ab#c", t = "ad#c"
Output: true
Explanation: Both s and t become "ac".

Example 2:
Input: s = "ab##", t = "c#d#"
Output: true
Explanation: Both s and t become "".

Example 3:
Input: s = "a#c", t = "b"
Output: false
Explanation: s becomes "c" while t becomes "b".
'''
def backspaceCompare(s, t):
    result1 = ''
    result2 = ''

    for fast1 in range(len(s)):
        if s[fast1] != '#':
            # result1.append(s[fast1])
            result1 += s[fast1]
        else:
            result1 = result1[:-1]

    for fast2 in range(len(t)):
        if t[fast2] != '#':
            # result2.append(t[fast2])
            result2 += t[fast2]

        else:
            result2 = result2[:-1]

    # a = ''.join(result1)
    # b = ''.join(result2)
    # print(result1)
    # print(result2)
    # print(result1==result2)
    return result1 == result2
backspaceCompare("xywrrmp","xywrrmu#p")

python
'''
977. Squares of a Sorted Array
Example 1:
Input: nums = [-4,-1,0,3,10]
Output: [0,1,9,16,100]
Explanation: After squaring, the array becomes [16,1,0,9,100].
After sorting, it becomes [0,1,9,16,100].

Example 2:
Input: nums = [-7,-3,2,3,11]
Output: [4,9,9,49,121]
'''
class Solution:
    def sortedSquares(self, nums: list[int]) -> list[int]:
        result = []
        for i in nums:
            j = i * i
            result.append(j)
        return sorted(result)
    
# 普通双指针    
def twoPointer(nums):
    

2022-11-26

双指针

python
'''
普通双指针
344. Reverse String
Example 1:
Input: s = ["h","e","l","l","o"]
Output: ["o","l","l","e","h"]

Example 2:
Input: s = ["H","a","n","n","a","h"]
Output: ["h","a","n","n","a","H"]
'''

class Solution:
    def reverseString(self, s: List[str]) -> None:
        """
        Do not return anything, modify s in-place instead.
        双指针法，定义左右指针，循环当左指针<右指针，
        交换左右值，再各自往中间走一步
        """
        left, right = 0, len(s)-1
        while left < right:
            s[left], s[right] = s[right], s[left]
            left += 1
            right -= 1

2022-11-27

其实很多数组填充类的问题，都可以先预先给数组扩容带填充后的大小，然后在从后向前进行操作。

避免了从前向后的索引移动产生多余的时间复杂度

python
'''
剑指Offer58-II.左旋转字符串
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如，输入字符串"abcdefg"和数字2，该函数将返回左旋转两位得到的结果"cdefgab"。

示例 1：
输入: s = "abcdefg", k = 2
输出: "cdefgab"

示例 2：
输入: s = "lrloseumgh", k = 6
输出: "umghlrlose"

限制：
1 <= k < s.length <= 10000
'''
# 反转前n的字符串，反转n-末尾的字符串，反转整个字符串
def leftReverse(s, n):
    li = list(s)
    li[:n] = reversed(li[:n])
    li[n:] = reversed(li[n:])
    li.reverse()
    return ''.join(li)
leftReverse("lrloseumgh", 6)

# 切片
def leftReverse(s, num):
     string = s[num:len(s)] + s[:num]
     return print(string)
leftReverse("lrloseumgh", 6)